Бісектри́са (лат. bis — двічі і лат. secare — розсікати, розтинати) — термін, що вживається вгеометрії для позначення кількох споріднених понять[1]:
- Бісектриса кута — промінь, що проходить через вершину кута і ділить його навпіл. Кожна точка бісектриси однаково віддалена від сторін кута.
- Бісектриса трикутника — відрізок бісектриси одного з кутів цього трикутника від вершини кута до перетину з протилежною стороною.
Властивості
- Теорема про бісектрису: Бісектриса внутрішнього кута трикутника ділить протилежну сторону у відношенні, рівному відношенню двох прилеглих сторін
- Бісектриси внутрішніх кутів трикутника перетинаються в одній точці — інцентрі — центрівписаного в цей трикутник кола.
- Бісектриси одного внутрішнього та двох зовнішніх кутів трикутника перетинаються в одній точці. Ця точка — центр одного з трьох зовнівписаних кіл цього трикутника.
- Основи бісектрис двох внутрішніх та одного зовнішнього кутів трикутника лежать на одній прямій, якщо бісектриса зовнішнього кута не є паралельною протилежній стороні трикутника.
- Якщо бісектриси зовнішніх кутів трикутника не паралельні протилежним сторонам, то їх основи лежать на одній прямій.
- Якщо в трикутнику дві бісектриси рівні, то трикутник — рівнобедрений (теорема Штейнера — Лемуса).
- Побудова трикутника за трьома заданим бісектрисами за допомогою циркуля та лінійки неможлива,[2] причому навіть за наявностітрисектора.[3]
- В рівносторонньому трикутнику бісектриса кута, протилежного до основи трикутника, є медіаною та висотою.
- Відстані від сторін кута до будь-якої точки бісектриси однакові.
- Кожна бісектриса трикутника ділиться точкою перетину бісектрис у відношенні суми довжин прилеглих сторін до довжини протилежної, рахуючи від вершини.
Формули за участю довжини бісектриси
Де:
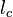 — бісектриса, проведена до сторони с
— бісектриса, проведена до сторони с — сторони трикутника проти вершин A, B,C відповідно
— сторони трикутника проти вершин A, B,C відповідно — довжини відрізків, на які бісектриса
— довжини відрізків, на які бісектриса 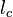 ділить сторону с
ділить сторону с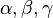 — внутрішні кути трикутника, що лежать навпроти сторін а, b,c відповідно
— внутрішні кути трикутника, що лежать навпроти сторін а, b,c відповідно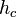 — висота трикутника, опущена на сторону c.
— висота трикутника, опущена на сторону c.
Задачі на властивість бісектрис трикутника
1. BD-бісектриса кута В трикутника АВС. Знайти:
1)відрізки AD і DC,якщо АВ=8см, ВС=14см, АС=11см;
2)сторону АВ, якщo AD : DC = 7:8, BC =24см;
3)сторону АС ,якщо АВ: ВС=2:3,CD-AD=3см;
4)сторони АВ,ВС і АС,якщо АВ +ВС=56см, AD=9см, DC=15см.
2.Точка D лежить на стороні АВ трикутника АВС.
Порівняти кути ACD і BCD,якщо АС=12см,ВС= 15 см,AD=6смBD=12см.
3.Бісектриса гострого кута гострого кута прямокутного трикутника ділить протилежний катет у відношенні 2:1.Знайти гострі кути трикутника.
4.Бісектриса прямого кута прямокутного трикутника ділить гіпотенузу на відрізки довжиною 15см і 20см.Знайти катети.
5.Бісектриса гострого кута прямокутного трикутника ділить катет у відношенні 5:3,а різниця цих відрізків дорівнює 6см.Знайти сторони трикутника.
6.Висота BD трикутника АВС дорівнює 24см і ділить сторону АС на відрізки
AD=7см i DC=10см. На які відрізки ділить сторону АС бісектриса кута В?
7.Периметр прямокутника дорівнює 42см ,а його діагональ ділиться бісектрисою прямого кута на відрізки,довжини яких відносяться як3:4.Знайти діагональ прямокутника.
8.Бісектриса кута прямокутника ділить його сторону на відрізки довжиною 10см і 14см,починаючи від найближчої до цього кута вершини. На які відрізки ділить ця бісектриса діагональ прямокутника.
9.Діагональ рівнобічної трапеції ділить висоту,проведену з вершини тупого кута,на відрізки довжиною 15см і 12см,а бічна сторона трапеції дорівнює її меншій основі. Знайти сторони трапеції.
10.У трикутник АВС вписано ромб ADEF так,що кут А у них спільний, а вершина Е належить стороні ВС.З найти довжини відрізків ВЕ і ЕС,якщо АВ=21см, ВС=18см, АС=15см.



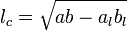


Це матеріал для класу поглибленого вивчення?
ВідповістиВидалити