
Висота́ трику́тника — відрізок, проведений з вершини кута до протилежної сторони або до продовження протилежної сторони і лежить на прямій, перпендикулярній до цієї сторони. Ця сторона називається основою трикутника. Точка перетину сторони і перпендикуляра називається основою перпендикуляра. Довжина висоти — це відстань від вершини до основи трикутника.
Висоту використовують для обчислення площі трикутника: половина добутку довжини висоти на довжину основи дорівнює площі трикутника.
- де h — висота трикутника, опущена на сторону.
В рівнобедреному трикутнику (трикутник в якому дві сторони конгруентні) висота проведена до неконгруентної сторони ділить цю сторону на дві рівні частини. В прямокутному трикутнику висота опущена на гіпотенузу ділить її на два відрізки, нехай це буде p і q. Якщо ми позначимо довжину висоти літерою h то отримаємо співвідношення:
Три висоти перетинаються в одній точці, яка називається ортоцентром трикутника. Ортоцентр лежить всередині трикутника (і відповідно всі основи перпендикулярів лежать в трикутнику) тоді і тільки тоді, якщо трикутник не тупокутний (в ньому жоден з внутрішніх кутів не більший за прямий кут). Дивіться також ортоцентрична система.

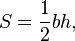
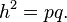
Немає коментарів:
Дописати коментар