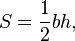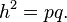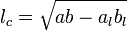субота, 10 січня 2015 р.

7 клас

пʼятниця, 2 січня 2015 р.

Висота́ трику́тника

Ортоцентр — точка де перетинаються три висоти трикутника

Висота́ трику́тника — відрізок, проведений з вершини кута до протилежної сторони або до продовження протилежної сторони і лежить на прямій, перпендикулярній до цієї сторони. Ця сторона називається основою трикутника. Точка перетину сторони і перпендикуляра називається основою перпендикуляра. Довжина висоти — це відстань від вершини до основи трикутника.

Висоту використовують для обчислення площі трикутника: половина добутку довжини висоти на довжину основи дорівнює площі трикутника.

S=\frac{1}{2}bh,

де h — висота трикутника, опущена на сторону.

В рівнобедреному трикутнику (трикутник в якому дві сторони конгруентні) висота проведена до неконгруентної сторони ділить цю сторону на дві рівні частини. В прямокутному трикутнику висота опущена на гіпотенузу ділить її на два відрізки, нехай це буде p і q. Якщо ми позначимо довжину висоти літерою h то отримаємо співвідношення:

h^2 = pq.

Три висоти перетинаються в одній точці, яка називається ортоцентром трикутника. Ортоцентр лежить всередині трикутника (і відповідно всі основи перпендикулярів лежать в трикутнику) тоді і тільки тоді, якщо трикутник не тупокутний (в ньому жоден з внутрішніх кутів не більший за прямий кут). Дивіться також ортоцентрична система.

Властивості бісектриси трикутника

Бісектри́са (лат. bis — двічі і лат. secare — розсікати, розтинати) — термін, що вживається вгеометрії для позначення кількох споріднених понять^[1]:

Бісектриса кута — промінь, що проходить через вершину кута і ділить його навпіл. Кожна точка бісектриси однаково віддалена від сторін кута.
Бісектриса трикутника — відрізок бісектриси одного з кутів цього трикутника від вершини кута до перетину з протилежною стороною.

Зміст

Властивості

Побудова бісектриси

Теорема про бісектрису: Бісектриса внутрішнього кута трикутника ділить протилежну сторону у відношенні, рівному відношенню двох прилеглих сторін
Бісектриси внутрішніх кутів трикутника перетинаються в одній точці — інцентрі — центрівписаного в цей трикутник кола.
Бісектриси одного внутрішнього та двох зовнішніх кутів трикутника перетинаються в одній точці. Ця точка — центр одного з трьох зовнівписаних кіл цього трикутника.
Основи бісектрис двох внутрішніх та одного зовнішнього кутів трикутника лежать на одній прямій, якщо бісектриса зовнішнього кута не є паралельною протилежній стороні трикутника.
Якщо бісектриси зовнішніх кутів трикутника не паралельні протилежним сторонам, то їх основи лежать на одній прямій.
Якщо в трикутнику дві бісектриси рівні, то трикутник — рівнобедрений (теорема Штейнера — Лемуса).
Побудова трикутника за трьома заданим бісектрисами за допомогою циркуля та лінійки неможлива,^[2] причому навіть за наявностітрисектора.^[3]
В рівносторонньому трикутнику бісектриса кута, протилежного до основи трикутника, є медіаною та висотою.
Відстані від сторін кута до будь-якої точки бісектриси однакові.
Кожна бісектриса трикутника ділиться точкою перетину бісектрис у відношенні суми довжин прилеглих сторін до довжини протилежної, рахуючи від вершини.

Формули за участю довжини бісектриси

Бісектриса трикутника. Виконується співвідношення BD: DC = AB: AC

l_c = {\sqrt{ab(a+b+c)(a+b-c)}\over{a+b}}

l_c = \sqrt{ab-a_lb_l}

l_c = \frac {2ab\cos\frac{\gamma}{2}}{a+b}

l_c = \frac {h_c}{\cos \frac {\alpha-\beta}{2}}

Де:

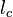$l_c$ — бісектриса, проведена до сторони с
$a, b, c$ — сторони трикутника проти вершин A, B,C відповідно
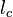$a_l, b_l$ — довжини відрізків, на які бісектриса $l_c$ ділить сторону с
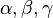$\alpha, \beta, \gamma$ — внутрішні кути трикутника, що лежать навпроти сторін а, b,c відповідно
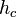$h_c$ — висота трикутника, опущена на сторону c.

Задачі на властивість бісектрис трикутника

1. BD-бісектриса кута В трикутника АВС. Знайти:

1)відрізки AD і DC,якщо АВ=8см, ВС=14см, АС=11см;

2)сторону АВ, якщo AD : DC = 7:8, BC =24см;

3)сторону АС ,якщо АВ: ВС=2:3,CD-AD=3см;

4)сторони АВ,ВС і АС,якщо АВ +ВС=56см, AD=9см, DC=15см.

2.Точка D лежить на стороні АВ трикутника АВС.

Порівняти кути ACD і BCD,якщо АС=12см,ВС= 15 см,AD=6смBD=12см.

3.Бісектриса гострого кута гострого кута прямокутного трикутника ділить протилежний катет у відношенні 2:1.Знайти гострі кути трикутника.

4.Бісектриса прямого кута прямокутного трикутника ділить гіпотенузу на відрізки довжиною 15см і 20см.Знайти катети.

5.Бісектриса гострого кута прямокутного трикутника ділить катет у відношенні 5:3,а різниця цих відрізків дорівнює 6см.Знайти сторони трикутника.

6.Висота BD трикутника АВС дорівнює 24см і ділить сторону АС на відрізки

AD=7см i DC=10см. На які відрізки ділить сторону АС бісектриса кута В?

7.Периметр прямокутника дорівнює 42см ,а його діагональ ділиться бісектрисою прямого кута на відрізки,довжини яких відносяться як3:4.Знайти діагональ прямокутника.

8.Бісектриса кута прямокутника ділить його сторону на відрізки довжиною 10см і 14см,починаючи від найближчої до цього кута вершини. На які відрізки ділить ця бісектриса діагональ прямокутника.

9.Діагональ рівнобічної трапеції ділить висоту,проведену з вершини тупого кута,на відрізки довжиною 15см і 12см,а бічна сторона трапеції дорівнює її меншій основі. Знайти сторони трапеції.

10.У трикутник АВС вписано ромб ADEF так,що кут А у них спільний, а вершина Е належить стороні ВС.З найти довжини відрізків ВЕ і ЕС,якщо АВ=21см, ВС=18см, АС=15см.

Збірник задач «Різносторонній трикутник»

Запитання для "геометричного" штурму опорних знань учнів :

Граємо в "да-ні":

Чи рівні усі кути, якщо не рівні бісектриси трикутника?
Чи рівні усі бісектриси, якщо рівні висоти трикутника?
Чи рівний кут 100⁰між бісектрисами рівнобедреного прямокутного трикутника?
Чи рівні усі кути тупокутного різностороннього трикутника?
Чи вдвічі більший катет прямокутного трикутника з гострим кутом 60⁰?
Чи завжди рівні відстані від будь-яких двох точок прямої до паралельної прямої?
Чи завжди радіус перпендикулярний до хорди, яку ділить навпіл?
Чи хорда, яку діаметр поділив навпіл, перпендикулярна до діаметру?
Чи дотична до кола може мати три точки дотику?
Чи завжди дотична перпендикулярна до будь-якого діаметра кола?
Дві прямі мають однакову спільну точку з колом. Чи вірно, що ці прямі січні для цього кола?
Чи в усіх прямокутних трикутниках менша бісектриса рівна половині гіпотенузи?
Із одної точки до кола проведені дві дотичні. Чи рівні відрізки цих дотичних?
Чи завжди навколо трикутника можна описати коло?
Чи завжди в трикутник можна вписати коло?
Чи завжди висоти трикутника перетинаються в одній точці, що лежить у вершині трикутника?
Чи завжди бісектриси перетинаються в одній точці?

ЗАДАЧІ

1. Сторони трикутника відносяться, як 3:4:5. Побудувати бісектриси трикутника і вписане коло. В якому відношенні до сторін знаходиться радіус вписаного кола.

2. Накресли прямокутний рівнобедрений трикутник. Проведи в ньому бісектриси. Вкажи центр вписаного в цей трикутник кола. Побудуй вписане коло.

3. Середня лінія трикутника утворює з прилеглими сторонами кут 45⁰. Який вид цього трикутника? Де знаходиться центр вписаного кола. Побудуй це коло.

Я дуже схильний вважати, що процес наукового відкриття можна розглядати як одну з форм мистецтва... Теоретик-математик на основі визначених припущень і згідно з добре встановленими логічними законами крок за кроком будує величну споруду, виявляючи силою своєї уяви невідомі співвідношення між її частинами. Добре побудована теорія в деяких відношеннях, безсумнівно, є твором мистецтва .

Е. Резерфорд

4. Трикутники АВС і МАВ рівні. Чи рівні відповідні радіуси вписаних кіл цих трикутників?

5. Трикутник КМN, К=90°, а = 3 см, b = 4 см, c = 5 см. Знайди радіус вписаного кола в трикутник АВС.

7. У рівнобедреного трикутника АВС знайди довжину радіуса, якщо бічна СВ = 43 м, АВ = 10 м.

9. Чи може центр вписаного кола лежати на середній лінії?

10. Знайти кути прямокутного трикутника, якщо центр вписаного кола лежить на висоті трикутника.

11. Обчислити радіус вписаного кола для трикутника, знаючи, сторони трикутника: 1) 2, 8, 4; 2) 4, 3, 5; 3) 2, 3, 5;, 4) 2, 7, 3; б) 8, б, 5. Знайти довжини відрізків, на які ділиться кожна сторона трикутника точкою дотику.

12. Накресліть будь-який тупокутний різносторонній трикутник. Який вид трикутника утворили точки дотику кола і трикутника?

13. Для яких трикутників центр вписаного кола лежать на перетині медіан?

14. У трикутника три рівні середні лінії. Де лежить центр вписаного кола? Як відноситься середня лінія до радіуса вписаного кола?

15. У трикутника , що утворений точками дотику даного трикутника і вписаного кола, рівносторонній. Чи може даний трикутник бути тупокутнім рівностороннім? (прямокутним рівностороннім?)

16. Периметр рівнобедреного трикутника 18 см, бічна сторона на 3 см довша від основи. Знайти радіус вписаного кола для трикутника, який утворений точками дотику вписаного кола і даного трикутника.

Завдання для самостійного закріплення умінь та навичок досліджувати та аналізувати навчальний матеріал

1.Який вид трикутника можна утворити, маючи лише радіус вписаного в трикутник кола?

2.У тупокутних трикутників точка дотику вписаного кола і сторони ділить цю сторону навпіл. Який вид цього трикутника? Де знаходиться центр вписаного кола?

3.Чи завжди будь-який відрізок може бути радіусом вписаного кола трикутника?

4.Чи радіуси вписаних кіл у нерівних трикутників можуть виявитися рівними?

5.Відновити на довільному тупокутному трикутнику вписане коло.

6. Визначити довжини радіусів вписаних кіл для трикутників, у яких величини сторін: а)46м, 46м, 19м. б)35м,35м,35м. в) 7м, 7м, 9м.

7.Скільки тупокутних трикутників можуть мати радіус вписаного кола 1 м?

8.Чи існують трикутники, у яких найменша сторона точкою дотику вписаного кола ділиться навпіл?

9.Яка довжина радіуса вписаного кола в трикутнику АВС, якщо:

1) а = 51 см; b =36 cм; с = 47 см?

2) а = 68 см; b = 56 cм, с = 58 см?

3) а = 5 см; b = 8 cм, с = 7 см?

4) а = 58 см; b = 58 cм, с = 59 см?

5) а = 5 см; b = 5 cм, с = 5 см?

Задачі для самостійних дослідів учнів.

1.Чи існує вид прямокутного трикутника, щоб довжина радіуса вписаного кола була рівна довжині середньої лінії, що проведена до найбільшої сторони?

2.Які існують види трикутників , у яких середня лінія не рівна радіусу вписаного кола? Замалювати кожний можливий випадок.

Збірник задач «Різносторонній трикутник»

1. Сторони трикутника дорівнюють 30 і 40 см, а висота , опущена на третю сторону дорівнює 24 см. Знайти медіану , проведену до третьої сторони трикутника.

2. Сторони трикутника дорівнюють 25 см, 24 см і 7 см. Знайти радіус описаного кола.

3. Сторони трикутника дорівнюють 3 і 5 см, а кут між ними 120 град. Знайдіть сторони подібного йому трикутника, периметр якого дорівнює 60 см.

4. Сторона трикутника дорівнює 35 см, а дві інші сторони утворюють кут 120 град. і відносяться, як 5:3. Обчислити периметр трикутника.

5. Сума двох сторін трикутника дорівнює 8 см, а кут між ними – 120 град. Знайти периметр трикутника, якщо третя сторона дорівнює 7 см.

6. Сторони трикутника, кут між якими 60 град., відносяться як 5:6, а третя сторона дорівнює 21 см. Обчислити периметр трикутника.

7. Сторони трикутника відносяться, як 5:4:2. Знайти сторони подібного трикутника, сума найбільшої та найменшої сторін якого дорівнює 21 см.

8. Сторони трикутника дорівнюють 14 см, 18 см і 28 см. Знайти медіану трикутника, опущену на більшу сторону.

9. Сума двох сторін трикутника дорівнює 65 см. Бісектриса між цими сторонами ділить протилежну сторону на відрізки 15 см і 24 см. Знайти всі сторони трикутника.

10. Дві сторони трикутника дорівнюють 3 і 7 см. Кут, протилежний до більшої з них, дорівнює 60 град. Знайти довжину третьої сторони трикутника.

11. Дві сторони трикутника відносяться, як 5:8. Висота, проведена до третьої сторони, ділить її на відрізки 7 см і 32 см. Знайти сторони трикутника.

12. Дві сторони трикутника дорівнюють 15 см і 20 см. Бісектриса кута між даними сторонами ділить третю сторону на відрізки, різниця між якими 4 см. Знайти периметр трикутника.

13. Висота трикутника, опущена на сторону, ділить її на відрізки 7 см і 32 см, а бісектриса ділить цю сторону на відрізки у відношенні 5:8. Обчислити периметр трикутника.

14. В коло радіуса R вписано трикутник з кутами 15 і 60 град. Знайти площу трикутника.

15. У трикутнику основа дорівнює 60 см, висота 12 см і медіана, проведена до основи , 13 см. Знайти бічні сторони.

16. У трикутнику одна із сторін дорівнює 1м, а прилеглі до неї кути дорівнюють 30 і 45 град. Зайти інші сторони трикутника.

17. З однієї вершини трикутника проведено висоту, бісектрису і медіану. Відтань від другої вершини до кінців висоти, бісектриси і медіани відповідно дорівнюють 21 см, 25 см і 25,5 см. Знайти периметр трикутника.

18. Знайти радіуси вписаного й описаного кола трикутника із сторонами 4 см, 5см і 7см.

19. Різниця двох кутів трикутника дорівнює 10 град., а кут між бісектрисами, проведеними з вершин цих кутів, дорівнює 115 град. Знайти ці кути.

20. Бісектриса кута при основі рівнобедреного трикутника ділить медіану, проведену до основи, на відрізки 10 см і 6 см. Обчислити периметр трикутника.

21. Периметр трикутника дорівнює 45 см , а його сторони відносяться, як 4:5:6. Знайти найбільшу сторону трикутника.

22. Медіана трикутника, проведена до сторони, довжина якої 20 см, утворює з нею кут 60 град., а сторона, що лежить проти цього кута, дорівнює

см. Знайти третю сторону трикутника.

23. Висота, проведена до основи трикутника, дорівнює 72см і ділить основу на відрізки 30см і 96см. Обчислити радіус описаного кола.

24. Бічні сторони трикутника дорівнюють 25 і 40см, а висота, проведена до основи, - 24см. Обчисліть площі частин трикутника , на які його ділить бісектриса, проведена до основи.

25. Медіани трикутника дорівнюють 24, 30 і 18см. Знайти площу трикутника.

26. Основа трикутника дорівнює 20см; медіани бічних сторін дорівнюють 18 і 24см. Знайти площу трикутника.

27. Знайти площу трикутника, якщо дві його сторони дорівнюють n і m, а медіана третьої сторони дорівнює k.

28. Сторони трикутника дорівнюють 10, 13 і 16см. Знайдіть сторони подібного йому трикутника, якщо сума найбільшої і найменшої сторін трикутника дорівнює 78см.

29. Сторони трикутника дорівнюють 24см і 40см, а кут між ними дорівнює 120⁰. Знайдіть відрізки, на які бісектриса данного кута ділить третю сторону.

30. Сторона трикутника дорівнює 56см. До неї проведено медіану і висоту, відстань між основами яких дорівнює 8см. Більша з двох інших сторін дорівнює 60см. Обчисліть діаметр описаного кола.

31. До основи трикутника проведено бісектрису, яка ділить її на відрізки 15 і 24см. Менша бічна сторона трикутника дорівнює 25см. Обчисліть площу трикутника.

32. Дві бічні сторони трикутника дорівнюють 78 і 20см, а висота, проведена до основи, дорівнює 72см. Обчисліть радіус описаного кола.

7 клас ГЕОМЕТРІЯ. Дистанційне навчання

субота, 10 січня 2015 р.

Розв’язування задач геометричного змісту та задач на пропорційний поділ

Конспект уроку на тему "Трикутник. Види трикутника"

7 клас

пʼятниця, 2 січня 2015 р.

Висота́ трику́тника

Властивості бісектриси трикутника

Зміст

Властивості

Формули за участю довжини бісектриси

Збірник задач «Різносторонній трикутник»

субота, 10 січня 2015 р.

Розв’язування задач геометричного змісту та задач на пропорційний поділ

Конспект уроку на тему "Трикутник. Види трикутника"

7 клас

пʼятниця, 2 січня 2015 р.

Висота́ трику́тника

Властивості бісектриси трикутника

Зміст

Властивості

Формули за участю довжини бісектриси

Збірник задач «Різносторонній трикутник»

субота, 10 січня 2015 р.

пʼятниця, 2 січня 2015 р.