Відрізок , кут, промінь

Отрезок, угол, луч

Отрезок - часть прямой, ограниченная двумя точками (концы отрезка)

Длина отрезка - положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке. Длину отрезка АВ также называют расстоянием ммежду точками А и В.
Свойства:
1) Длины равных отрезков равны
2) Длина суммы отрезков равнв сумме их длин

Луч (полупрямая) – часть прямой, имеющая начало и не имеющая конца.

Угол - фигура образованная двумя лучами, исходящими из одной точки (вершина угла). Общая вершина называется вершиной угла, а лучи - сторонами угла.
Обычно под углом понимают плоский угол, но есть другие виды углов - многогранные.

Виды углов

Острый	Прямой	Тупой	Развёрнутый

Угол, меньший прямого, называется острым.

Угол, равный смежному с ним, называется прямым.

Угол, больший прямого, называется тупым.

Угол называется развёр-нутым, если его стороны сместе составляют прямую.

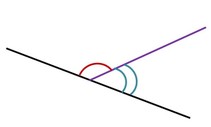Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.
Теорема. Сумма смежных углов равна 180°.
Следствие. Если смежные углы равны, то они прямые.

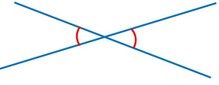Два угла называютсявертикальными, если стороны одного угла являются продолжениями сторон другого.
Теорема. Вертикальные углы равны.
Угловая мера меньшего из вертикальных углов называется углом между прямыми.

Итак, сформулируем определения понятий луча, отрезка и фигуры:
• Лучом называется часть прямой, ограниченная одной из её точек.
• Отрезком называется часть прямой, заключенная между двумя её точками.
• Под фигурой понимают некоторое сочетание определенным образом расположенных в одной плоскости (а иногда и в пространстве) элементов: точек, прямых, лучей, отрезков (иногда и плоскостей). 

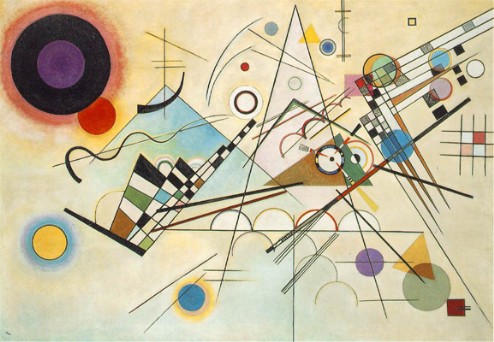
Найди разные виды углов на рисунке и картине:

Из истории. Единицы измерения углов.
Градусное измерение углов возникло в Древнем Вавилоне задолго до новой эры. Жрецы считали, что свой дневной путь Солнце совершает за 180 «шагов», и, значит, один «шаг» равен 1/180 развернутого угла.
В Вавилоне была принята шестидесятиричная система счисления, т. е. фактически числа записывались в виде суммы степеней числа 60, а не 10, как это принято в нашей десятеричной системе. Естественно поэтому, что для введения более мелких единиц измерения углов один «шаг» последовательно делился на 60 частей.

Вавилонская система измерения углов оказалась достаточно удобной, и ее сохранили математики Греции и Рима. 
Термины, которыми мы пользуемся для названия угловых величин, имеют латинские корни. Слово «градус» происходит от латинского gradus (шаг, ступень). В переводе с латинского minutus означает «уменьшенный». Наконец, secunda переводится как «вторая». Имеется в виду следующее: деление градуса на 60 частей, т. е. минуты,— это первое деление; деление минуты на 60 секунд — второе деление градуса. Малоупотребительное название 1/60  секунды — терцина, латинское tercina означает «третье» (деление градуса).

Принятая сейчас система обозначения величин углов получила широкое распространение на рубеже XVI и XVII вв.; ею уже пользовались такие известные астрономы, как Н. Коперник и Т. Браге. Но еще К. Птолемей (II в. н. э.) количество градусов обозначал кружком, число минут — штрихом, а секунд — двумя штрихами.

Другая единица измерения углов — радиан — введена совсем недавно. Первое издание (это были экзаменационные билеты), содержащее термин «радиан», появилось в 1873 г. в Англии. Сначала в обозначениях указывалось, что имеется в виду радианная мера , но вскоре инадекс R (или г) стали опускать. Сам термин «радиан» происходит от латинского radius (спица, луч).

Если вспомнить определение угла в один радиан (центральный угол, длина дуги которого равна радиусу окружности), то выбор корня «рад» для названия такого угла представляется совершенно естественным. 

Завдання для самостійного опрацювання

Знайти невідомі кути у таких композицій фігур

Зразок завдання

Знайти самостійно невідомі кути у фігурах

Перевірте правильність величин кутів в трикутниках