Порядком квадрата, розбитого на складені квадрати, називається
число складових його квадратів.


Розбиття квадрата, ніяка підмножина квадратів якого не
утворює прямокутника (не рахуючи окремих квадратів), називається простим.


Коротка історія
Найперші знайдені Бруксом, Смітом, Стоуном і Таттом
довершені квадрати були 69-го порядку. У 1939 році Р.
Шпраг (R. Sprague) знайшов довершений квадрат 55-го порядку, це був перший
опублікований довершений квадрат. Пізніше за Т. Р. Уїллкокс
(T. H. Willcocks) знайшов довершений квадрат 24-го порядку, який
довгий час тримав рекорд трохи порядку.
Нарешті, в 1978 році голландський математик А. Й. У.
Дуйвестейн (A. J. W. Duijvestijn) за допомогою комп'ютера знайшов
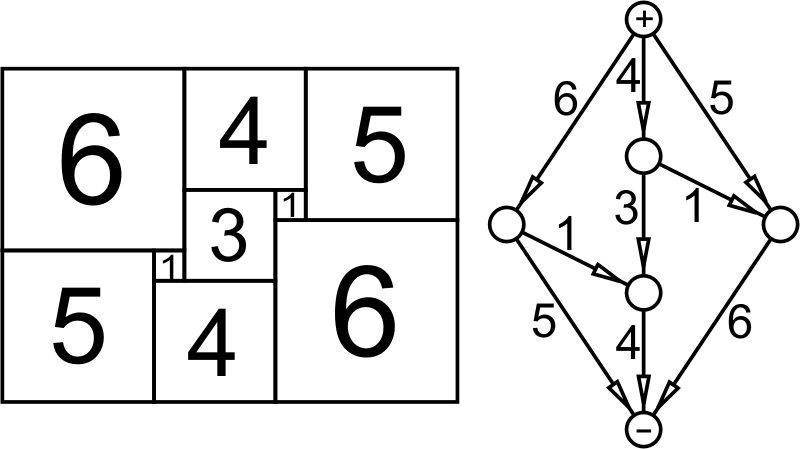
розбиття квадрата на 21 квадрат, серед яких немає рівних. Він довів, що не
існує довершеного квадрата меншого порядку, а також показав, що знайдене ним
розбиття — єдино можливе для 21-го порядку.
Разбиение квадрата на 21 квадрат, средикоторых нет равных. Цифра внутри каждогоквадрата означает длину его стороны.Соответственно, длина стороны большогоквадрата равна (складывая длины сторонкрайних квадратов) 50 + 35 + 27 =50 + 29 + 33 = 33 + 37 + 42 =27 + 19 + 24 + 42 = 112
Квадри́рование квадра́та — задача о разбиении квадрата на конечное число меньших квадратов. В болееузком смысле — задача о разбиении квадрата на конечное число попарно неравных между собой квадратов.
Долгое время считалось, что эта чрезвычайно трудная математическая задача неразрешима. В 1936—1938 годах её решили четыре студента Тринити-колледжа Кембриджского университета [1].
Кубирование куба
«Кубирование куба», то есть разбиение куба на конечное число попарно неравных между собой кубовневозможно. Доказательство этого факта было дано Бруксом, Смитом, Стоуном и Таттом.
Идея доказательства состоит в следующем. Допустим, что искомое разбиение куба существует. Среди всехкубов разбиения, стоящих на нижнем основании исходного куба, выберем наименьший. Назовём его кубомA. Поскольку к A прилегают с боков только бо́льшие кубы разбиения, их грани будут возвышаться над ним совсех сторон, образуя «стены». Отсюда ясно, что на верхнем основании A могут стоять только кубы меньшихразмеров.
Выберем среди них наименьший и обозначим его B. При этом, B не может стоять на краю куба A, так как приквадрировании квадрата наименьший квадрат не может быть с краю.
Повторяя для него те же рассуждения, что и для A, приходим к выводу о существовании ещё меньшего кубаC, стоящего на верхнем основании B. Повторяя эти рассуждения, мы получаем бесконечнуюпоследовательность кубов разбиения, что противоречит нашему предположению о конечности разбиения.
Аналогично, невозможно «гиперкубирование гиперкуба» для гиперкубов любой размерности, большей 3-х.Действительно, для любой размерности n гиперкубы разбиения, прилегающие к какой-либо (n − 1)-мернойгиперграни исходного гиперкуба, должны разбивать эту гипергрань на конечное число попарно неравных(n − 1)-мерных гиперкубов. При n = 4 «гиперкубирование» невозможно, так как должно порождать«кубирование» 3-мерных гиперграней исходного 4-мерного гиперкуба. Индукцией по n можно сделатьзаключение о невозможности «гиперкубирования» для всех n > 3.


Немає коментарів:
Дописати коментар