Властивості кутів, що вписані в коло
Основні означення.
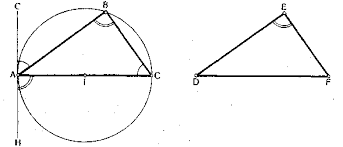
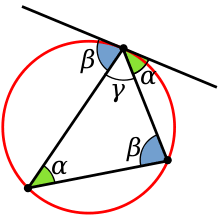

2.Знайти рівні кути на колі.

3.Знайти рівні кути на колі.

4.Знайти рівні кути на колі.
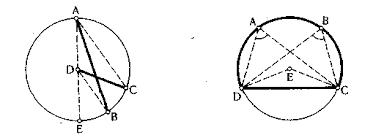
5.Знайти рівні кути на колі.
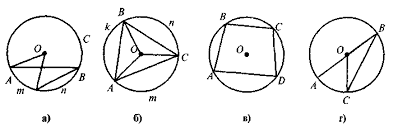
6.Знайти рівні кути на колі.
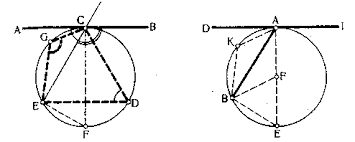
7.Знайти рівні кути на колі.

Завдання для самостійного опрацювання.
Основні означення.
- Коло-геометрична фігура, яка складається з усіх точок, розміщених на даній відстані (вона називається радіусом) від даної точки(центра);
- Хорда-відрізок,що сполучає дві точки кола;
- діаметр-хорда,що проходить через центр кола;
- дуга-частина кола між двома його точками
- Круг-частина площини,обмежена колом
- Дотична до кола-прямя,що маєзколом тільки одну спільну точку(точка дотику)
- Дуга називається півколом,якщо відрізок,що сполучає її кінці,є діаметром
- Центральний кут-кут з вершиною в центрі кола;
- Вписаний кут-кут,вершина якого лежить на колі,а сторони перетинають коло.
Деякі властивості КОЛА
Через три точки, що не лежать на одній прямій, можна провести коло, і притому тільки одне.
Точка дотику двох кіл лежить на прямій, що проходить через їхні центри.
Відстань між колами, що не мають спільних точок – це відрізок, що лежить на прямій між двома колами, щопроходить через їхні центри.
Ізопериметрична нерівність: З усіх замкнутих кривих даної довжини коло обмежує область максимальної площі.
Вписаний кут або дорівнює половині центрального кута, що спирається на його дугу, або доповнює половину цього кута до 180°.
Два вписаних кути, що спираються на одну й ту ж дугу, рівні.
Вписаний кут, що спирається на дугу довжиною в половину кола дорівнює 90°.
Кут між двома січними, проведеними з точки, що лежить поза колом дорівнює піврізниці мір дуг, що лежать між січними.
Кут між хордами, що перетинаються дорівнює півсумі мір дуги, що лежить у куті і дуги навпроти неї.
Кут між дотичною та хордою дорівнює половині градусної міри дуги, що стягується хордою.
Відрізки дотичних до кола, проведених з однієї точки, рівні й утворюють рівні кути з прямою, що проходить через цю точку і центр кола.
При перетині двох хорд добуток відрізків, на які ділиться одна з них точкою перетину, дорівнює добутку відрізків на які ділиться інша.
Добуток довжин відстаней від обраної точки до двох точок перетину кола та січної, що проходить через обрану точку, не залежить від вибору січної і дорівнює абсолютній величині ступені точки відносно кола.
Квадрат довжини відрізка дотичної дорівнює добутку довжин відрізків січної і дорівнює абсолютній величині міри точки відносно кола.
Властивості хорд
Рівні дуги стягують рівні хорди; рівні хорди стягують рівни дуги
AB=CD, ÈAB=ÈCD
Паралельні хорди перетинають на колі рівні дуги
AB ||CD,ÈAD=ÈBC
Діаметр кола,перпендикулярний до хорди, проходить через її середину; діаметр кола, який проходить через середину хорди,перпендикулярний до неї
AB^ CD,AM=MB
Якщо дві хорди кола перетинаються ,то добуток відрізків однієї хорди дорівнює відрізків другої хорди
AM× BM=CM× DM
Якщо хорда і діаметр кола мають спільну вершину,то квадрат довжини хорди дорівнює добутку діаметра кола і проекції даної хорди на цей діаметр
AB2=AC× AD
BD2=AD ×CD
Задачі на побудову циркулем і лінійкою
Варіант 1
1. У трикутнику АВС кут А=50°, кут В=80°. Довести, що
а) трикутник АВС- рівнобедрений;
б)бісектриса зовнішнього кута трикутника паралельна основі;
в) АМ=ВС, якщо медіана СО продовжена на відрізок ОМ, рівний СО.
2. Побудувати трикутник, периметр якого дорівнює 18 см, відношення сторін 2 : 3 : 4. Описати навколо нього коло.
3. ΔАВС і ΔADC мають спільну сторону АС, АВ=ВС=СD=DA, точка F лежить на стороні АС. Довести, що
а)АВ|| СD і AD||BC;
б)BF=FD;
в)DB ^ AC;
г) точка F рівновіддалена від AB і АD.
Варіант 2
1. У трикутнику ЕМК ∠М=40°, ∠К=70°. Довести, що
а) Δ ЕМК - рівнобедрений;
б) промінь МС, проведений паралельно до основи, є бісектрисою зовнішнього кута;
в) висоти трикутника КА і ED рівні.
2. Побудувати ΔАВС, в якому ∠А : ∠В : ∠С = 1 : 2 : 3, АВ = 8 см. Вписати у побудований трикутник коло.
3. Δ KMS і Δ КМР мають спільну сторону МК, KS = MP, SM = KP. Довести, що
а) КР|| SM, KS || MP;
б) бісектриси кутів SA і РВ рівні;
в) SA||PB.
Довжина кола і площа круга
Довжину дуги кола з радіусом R, утвореного центральним кутом j, виміряним у радіанах, можна обчислити за формулою
L = Rj.
Довжину кола з радіусом R можна обчислити за формулою
C = 2πR. С» 6,28R
S = πR2= 0,25 πD2. S » 3,14R2.
де D = 2R ‒ діаметр.
Історична довідка.
Упродовж багатьох століть математиків цікавила задача про квадратуру кола: побудову за допомогою лінійки та циркуля квадрату з площею, що дорівнювала б площі круга. Ця задача не має розв'язку, оскільки число пі трансцедентне, що довів у 1882 Фердинанд фон Ліндеманн.
Задачі на малюнках.
Задачі на малюнках.
1.Знайти рівні кути на колі.
2.Знайти рівні кути на колі.
3.Знайти рівні кути на колі.
4.Знайти рівні кути на колі.
5.Знайти рівні кути на колі.
6.Знайти рівні кути на колі.
7.Знайти рівні кути на колі.
Завдання для самостійного опрацювання.
1. Визначити градусну міру кута, вписаного в коло, якщо відповідний йому центральний кут дорівнює:
1) 48°; 2)126°; 3)180°; 4)254°; 5)α.
2. Визначити градусну міру центрального кута, кола, якщо градусна міра відповідного йому вписаного кута дорівнює: 1)17°; 2)87°; 3)90°; 4)176°; 5)α.
3. Точка В кола і його центр О лежать по різні боки від хорди АС. Знайти: 1)кут АВС, якщо кутАОС = 124°;
2)кут АОС, якщо ÐАВС =94°.
4. Точки В і D лежать на колі по одну сторону від хорди АС, кутАВС =42°. Знайти кут АDС.
5. Точки В і D лежать на колі по різні боки від хорди АС, кутАВС = 78°. Знайти кут АDС.
6. Навколо трикутника АВС описано коло з центром О. Знайти кут ВОС, якщо: 1) кутА=78°; 2) кутА = 128°.
57. У трикутнику АВС кутА=36°, кутВ=78°, О- центр описаного кола. Знайти: кутАОВ, кутВОС, кутАОС.
58. Визначити кути рівнобедреного трикутника, вписаного в коло, бічна сторона якого стягує у дугу 38°.
59. Хорда ділить коло у відношенні 5:7. Визначити величини вписаних кутів, які спираються на цю хорду.
60. Хорда МN ділить коло на дві дуги. Градусна міра меншої з них дорівнює 140°, а більша ділиться точкою К у відношенні 5:6, починаючи від точки М. Знайти кутNМК.
61. Коло поділено трьома точками на частини, які відносяться між собою, як 3:5:7. Точки поділу сполучено між собою. Визначити кути утвореного трикутника.
62. Точки С і D кола лежать по один бік від діаметра АВ (мал.. 10). Знайти кут DСВ, якщо кутАСD = 41°.
63. Точки М і К кола лежать по один бік від діаметра СD. Знайти кут СDК, якщо ÐDМК = 53°.
64. Кут при вершині рівнобедреного трикутника дорівнює 78°. Півколо, побудоване на бічній стороні трикутника, як на діаметрі, ділиться іншими сторонами на три дуги. Скільки градусів містять ці дуги?


Коло на площині, даного радіуса r, у певній вибранійдекартовій системі координат x і y, з центром в точці (a, b) описується стандартним рівнянням кола:
(х - а)2 + (у - b)2 = R2,
де С(а; b) – центр кола, R – радіус кола.
У полярній системі координат рівняння кола має вигляд r = R.
Це рівняння випливає з теореми Піфагора, при її застовуванні до кожної точки кола, як показано на рисунку справа, де радіус це гіпотенуза прямокутного трикутника, катети якого x − a та y − b. Якщо центр кола знаходиться в початку координат (0, 0), тоді рівняння спрощується до такого вигляду:
х2 + у2 = R2,
Загальне рівняння кола:
ах2 + аy2 + dx + ey + f = 0,
де а≠0, d, e, f - відомі дійсні числа, х, у – змінні. Виділенням повних квадратів відносно змінної х та відносно змінної у, це рівняння можна звести до вигляду: (х - а)2 + (у - b)2 = R2.
Наприклад для рівняння: х2 + y2 + dx + ey + f = 0,
x2 + dx + 0,25d2 + y2+ ey+ 0,25e2 = −f+0,25d2+0,25e2
(x + 0,5d)2 + (y + 0,5e)2= −f + 0,25d2 + 0,25e2
Параметричне означення кола.
Коло на площині, даного радіуса r, у певній вибранійдекартовій системі координат x і y, описується системою рівнянь:
x = a + r*cost
y = b + r*sint
З геометричної точки зору це кут до осі x, променя проведеного з початку координат до точки (x, y). Якщо записати x та y через параметр t, отримаємо:
x = a + r(1 ‒ t2)(1 + t2)-1
y = b + 2rt(1 + t2)-1.
Полярні координати рівняння кола.
Рівняння кола в полярних координатах:
r2 ‒ 2rr0 cos(θ – φ) + r02 = a2
де a – радіус кола, r0 ‒ відстань від початкукоординат до центру кола та φ – кут відкладенийпроти годинникової стрілки від додатньої осі x до лініїщо з’єднує початок координат з центром кола.
Для кола, центр якого знаходиться в початку координат r0 = 0, це рівняння спрощується до виглядуr = a. Якщо r0 = a або якщо початок координат лежить на колі, тоді отримуємо рівняння:
r = 2acos(θ – φ).
В загальному випадку, рівняння можна розв’язати дляr:
r = 2r0cos(θ – φ)+( a2 ‒ r02sin2(θ – φ))0,5.
Дотичні і нормалі
(0,5А + х1)х + (0,5В + у1)у +( 0,5Ах1 + 0,5Ву1 + С) = 0,
де A, B і С ‒ коефіцієнти в загальному рівнянні кола.
(х ‒ х1)(2х1 + А)-1 = (у ‒ у1)(2у1 + В)-1.
Немає коментарів:
Дописати коментар