неділя, 19 квітня 2015 р.
Властивості кутів, що вписані в коло
Властивості кутів, що вписані в коло
Основні означення.
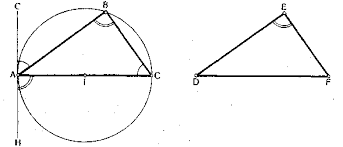
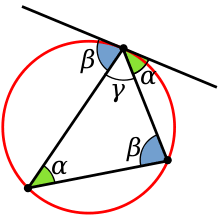

2.Знайти рівні кути на колі.

3.Знайти рівні кути на колі.

4.Знайти рівні кути на колі.
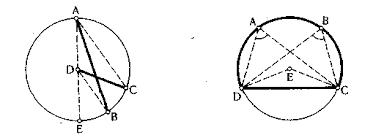
5.Знайти рівні кути на колі.
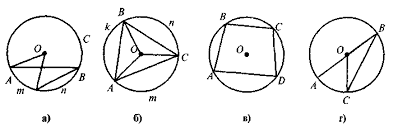
6.Знайти рівні кути на колі.
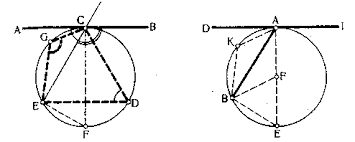
7.Знайти рівні кути на колі.

Завдання для самостійного опрацювання.
Основні означення.
- Коло-геометрична фігура, яка складається з усіх точок, розміщених на даній відстані (вона називається радіусом) від даної точки(центра);
- Хорда-відрізок,що сполучає дві точки кола;
- діаметр-хорда,що проходить через центр кола;
- дуга-частина кола між двома його точками
- Круг-частина площини,обмежена колом
- Дотична до кола-прямя,що маєзколом тільки одну спільну точку(точка дотику)
- Дуга називається півколом,якщо відрізок,що сполучає її кінці,є діаметром
- Центральний кут-кут з вершиною в центрі кола;
- Вписаний кут-кут,вершина якого лежить на колі,а сторони перетинають коло.
Деякі властивості КОЛА
Через три точки, що не лежать на одній прямій, можна провести коло, і притому тільки одне.
Точка дотику двох кіл лежить на прямій, що проходить через їхні центри.
Відстань між колами, що не мають спільних точок – це відрізок, що лежить на прямій між двома колами, щопроходить через їхні центри.
Ізопериметрична нерівність: З усіх замкнутих кривих даної довжини коло обмежує область максимальної площі.
Вписаний кут або дорівнює половині центрального кута, що спирається на його дугу, або доповнює половину цього кута до 180°.
Два вписаних кути, що спираються на одну й ту ж дугу, рівні.
Вписаний кут, що спирається на дугу довжиною в половину кола дорівнює 90°.
Кут між двома січними, проведеними з точки, що лежить поза колом дорівнює піврізниці мір дуг, що лежать між січними.
Кут між хордами, що перетинаються дорівнює півсумі мір дуги, що лежить у куті і дуги навпроти неї.
Кут між дотичною та хордою дорівнює половині градусної міри дуги, що стягується хордою.
Відрізки дотичних до кола, проведених з однієї точки, рівні й утворюють рівні кути з прямою, що проходить через цю точку і центр кола.
При перетині двох хорд добуток відрізків, на які ділиться одна з них точкою перетину, дорівнює добутку відрізків на які ділиться інша.
Добуток довжин відстаней від обраної точки до двох точок перетину кола та січної, що проходить через обрану точку, не залежить від вибору січної і дорівнює абсолютній величині ступені точки відносно кола.
Квадрат довжини відрізка дотичної дорівнює добутку довжин відрізків січної і дорівнює абсолютній величині міри точки відносно кола.
Властивості хорд
Рівні дуги стягують рівні хорди; рівні хорди стягують рівни дуги
AB=CD, ÈAB=ÈCD
Паралельні хорди перетинають на колі рівні дуги
AB ||CD,ÈAD=ÈBC
Діаметр кола,перпендикулярний до хорди, проходить через її середину; діаметр кола, який проходить через середину хорди,перпендикулярний до неї
AB^ CD,AM=MB
Якщо дві хорди кола перетинаються ,то добуток відрізків однієї хорди дорівнює відрізків другої хорди
AM× BM=CM× DM
Якщо хорда і діаметр кола мають спільну вершину,то квадрат довжини хорди дорівнює добутку діаметра кола і проекції даної хорди на цей діаметр
AB2=AC× AD
BD2=AD ×CD
Задачі на побудову циркулем і лінійкою
Варіант 1
1. У трикутнику АВС кут А=50°, кут В=80°. Довести, що
а) трикутник АВС- рівнобедрений;
б)бісектриса зовнішнього кута трикутника паралельна основі;
в) АМ=ВС, якщо медіана СО продовжена на відрізок ОМ, рівний СО.
2. Побудувати трикутник, периметр якого дорівнює 18 см, відношення сторін 2 : 3 : 4. Описати навколо нього коло.
3. ΔАВС і ΔADC мають спільну сторону АС, АВ=ВС=СD=DA, точка F лежить на стороні АС. Довести, що
а)АВ|| СD і AD||BC;
б)BF=FD;
в)DB ^ AC;
г) точка F рівновіддалена від AB і АD.
Варіант 2
1. У трикутнику ЕМК ∠М=40°, ∠К=70°. Довести, що
а) Δ ЕМК - рівнобедрений;
б) промінь МС, проведений паралельно до основи, є бісектрисою зовнішнього кута;
в) висоти трикутника КА і ED рівні.
2. Побудувати ΔАВС, в якому ∠А : ∠В : ∠С = 1 : 2 : 3, АВ = 8 см. Вписати у побудований трикутник коло.
3. Δ KMS і Δ КМР мають спільну сторону МК, KS = MP, SM = KP. Довести, що
а) КР|| SM, KS || MP;
б) бісектриси кутів SA і РВ рівні;
в) SA||PB.
Довжина кола і площа круга
Довжину дуги кола з радіусом R, утвореного центральним кутом j, виміряним у радіанах, можна обчислити за формулою
L = Rj.
Довжину кола з радіусом R можна обчислити за формулою
C = 2πR. С» 6,28R
S = πR2= 0,25 πD2. S » 3,14R2.
де D = 2R ‒ діаметр.
Історична довідка.
Упродовж багатьох століть математиків цікавила задача про квадратуру кола: побудову за допомогою лінійки та циркуля квадрату з площею, що дорівнювала б площі круга. Ця задача не має розв'язку, оскільки число пі трансцедентне, що довів у 1882 Фердинанд фон Ліндеманн.
Задачі на малюнках.
Задачі на малюнках.
1.Знайти рівні кути на колі.
2.Знайти рівні кути на колі.
3.Знайти рівні кути на колі.
4.Знайти рівні кути на колі.
5.Знайти рівні кути на колі.
6.Знайти рівні кути на колі.
7.Знайти рівні кути на колі.
Завдання для самостійного опрацювання.
1. Визначити градусну міру кута, вписаного в коло, якщо відповідний йому центральний кут дорівнює:
1) 48°; 2)126°; 3)180°; 4)254°; 5)α.
2. Визначити градусну міру центрального кута, кола, якщо градусна міра відповідного йому вписаного кута дорівнює: 1)17°; 2)87°; 3)90°; 4)176°; 5)α.
3. Точка В кола і його центр О лежать по різні боки від хорди АС. Знайти: 1)кут АВС, якщо кутАОС = 124°;
2)кут АОС, якщо ÐАВС =94°.
4. Точки В і D лежать на колі по одну сторону від хорди АС, кутАВС =42°. Знайти кут АDС.
5. Точки В і D лежать на колі по різні боки від хорди АС, кутАВС = 78°. Знайти кут АDС.
6. Навколо трикутника АВС описано коло з центром О. Знайти кут ВОС, якщо: 1) кутА=78°; 2) кутА = 128°.
57. У трикутнику АВС кутА=36°, кутВ=78°, О- центр описаного кола. Знайти: кутАОВ, кутВОС, кутАОС.
58. Визначити кути рівнобедреного трикутника, вписаного в коло, бічна сторона якого стягує у дугу 38°.
59. Хорда ділить коло у відношенні 5:7. Визначити величини вписаних кутів, які спираються на цю хорду.
60. Хорда МN ділить коло на дві дуги. Градусна міра меншої з них дорівнює 140°, а більша ділиться точкою К у відношенні 5:6, починаючи від точки М. Знайти кутNМК.
61. Коло поділено трьома точками на частини, які відносяться між собою, як 3:5:7. Точки поділу сполучено між собою. Визначити кути утвореного трикутника.
62. Точки С і D кола лежать по один бік від діаметра АВ (мал.. 10). Знайти кут DСВ, якщо кутАСD = 41°.
63. Точки М і К кола лежать по один бік від діаметра СD. Знайти кут СDК, якщо ÐDМК = 53°.
64. Кут при вершині рівнобедреного трикутника дорівнює 78°. Півколо, побудоване на бічній стороні трикутника, як на діаметрі, ділиться іншими сторонами на три дуги. Скільки градусів містять ці дуги?


Коло на площині, даного радіуса r, у певній вибранійдекартовій системі координат x і y, з центром в точці (a, b) описується стандартним рівнянням кола:
(х - а)2 + (у - b)2 = R2,
де С(а; b) – центр кола, R – радіус кола.
У полярній системі координат рівняння кола має вигляд r = R.
Це рівняння випливає з теореми Піфагора, при її застовуванні до кожної точки кола, як показано на рисунку справа, де радіус це гіпотенуза прямокутного трикутника, катети якого x − a та y − b. Якщо центр кола знаходиться в початку координат (0, 0), тоді рівняння спрощується до такого вигляду:
х2 + у2 = R2,
Загальне рівняння кола:
ах2 + аy2 + dx + ey + f = 0,
де а≠0, d, e, f - відомі дійсні числа, х, у – змінні. Виділенням повних квадратів відносно змінної х та відносно змінної у, це рівняння можна звести до вигляду: (х - а)2 + (у - b)2 = R2.
Наприклад для рівняння: х2 + y2 + dx + ey + f = 0,
x2 + dx + 0,25d2 + y2+ ey+ 0,25e2 = −f+0,25d2+0,25e2
(x + 0,5d)2 + (y + 0,5e)2= −f + 0,25d2 + 0,25e2
Параметричне означення кола.
Коло на площині, даного радіуса r, у певній вибранійдекартовій системі координат x і y, описується системою рівнянь:
x = a + r*cost
y = b + r*sint
З геометричної точки зору це кут до осі x, променя проведеного з початку координат до точки (x, y). Якщо записати x та y через параметр t, отримаємо:
x = a + r(1 ‒ t2)(1 + t2)-1
y = b + 2rt(1 + t2)-1.
Полярні координати рівняння кола.
Рівняння кола в полярних координатах:
r2 ‒ 2rr0 cos(θ – φ) + r02 = a2
де a – радіус кола, r0 ‒ відстань від початкукоординат до центру кола та φ – кут відкладенийпроти годинникової стрілки від додатньої осі x до лініїщо з’єднує початок координат з центром кола.
Для кола, центр якого знаходиться в початку координат r0 = 0, це рівняння спрощується до виглядуr = a. Якщо r0 = a або якщо початок координат лежить на колі, тоді отримуємо рівняння:
r = 2acos(θ – φ).
В загальному випадку, рівняння можна розв’язати дляr:
r = 2r0cos(θ – φ)+( a2 ‒ r02sin2(θ – φ))0,5.
Дотичні і нормалі
(0,5А + х1)х + (0,5В + у1)у +( 0,5Ах1 + 0,5Ву1 + С) = 0,
де A, B і С ‒ коефіцієнти в загальному рівнянні кола.
(х ‒ х1)(2х1 + А)-1 = (у ‒ у1)(2у1 + В)-1.
БАНК ЗАВДАНЬ для систематизації і повтерення
БАНК ЗАВДАНЬ для систематизації і повтерення
З ТЕМИ «НАЙПРОСТІШІ властивості ФІГУРИ »
Рівень А. Стандарт.
1. Наведіть приклади геометричних фігур, з яких складається квадрат. Які властивості квадрата вам відомі?
2. З чого складаються будь-які геометричні фігури?
3. Назвіть основні геометричні фігури на площині. Чи можна їх виміряти?
4. Із скількох точок складається відрізок? Чи може відрізок мати міру?
5. Із скількох точок складається пряма?
6. Із скількох точок складається промінь(півпряма)?
7. Як позначаються точки і прямі? Як на прямій позначити 1001 точку?
8. Скільки можна провести прямих через дві дані точки А та В? Скільки відрізків АВ можна розташувати на цій прямій?
9. Скільки можна провести прямих через три дані точки? Розгляньте різні випадки.
10. Скільки можна провести прямих через даний відрізок?
11. Чи можна провести пряму через два даних рівних відрізки?
12. Сформулюйте основні властивості належності точок і прямих.
13. Скільки точок перетину можуть утворити чотири прямі? Розгляньте усі випадки?
Тест "ТОЧКА І ПРЯМА".
1. Яке з тверджень правильне?
Геометрія - це наука про:
Геометрія - це наука про:
А) вимірювання на місцевості;
Б) доведення геометричних тверджень;
В) побудови геометричних фігур;
Г) властивості геометричних фігур.
2. Яке з тверджень правильне?
Геометричною фігурою є:
Геометричною фігурою є:
А) частина площини або прямої;
Б) спільна частина двох будь-яких предметів;
В) будь-яка сукупність точок;
Г) об'єднання кількох геометричних фігур.
3. На прямій a та b поставте точки М, К, Р, А, О.
Яке з тверджень неправильне?
Яке з тверджень неправильне?
А) Точки М, О, Р належать прямій а.
Б) Точка О - точка перетину прямих а, b.
В) Пряма а проходить через точки А, О, Р, М.
4) Точки А, О, К належать прямій b.
4. Які з тверджень є основними властивостями належності точок і прямих на площині?
А) Дві різні прямі можуть не перетинатися.
Б) Існує безліч точок, що не належать прямій.
В) Вершини многокутника належать прямим, що містять його сторони.
Г) Через будь-які дві точки можна провести пряму і тількиодну.
5. Скільки різних прямих в даній площині можна провести через чотири точки, ніякі три з яких не лежать на одній прямій?
А) шість; Б) п'ять; В) чотири; Г) дві.
6. Накреслити трикутник і поставте на його сторонах точки S,N, Р. Знайдіть неправильне твердження:
А) Точка S розділяє відрізок А і В на рівні частини.
Б) Точки відрізка NP належать одній з двох півплощин, на які пряма ВС розбиває площину.
В) Відрізок SN перетинається з прямими АВ і ВС.
Г) Точка Р не лежить між точками А і С.
7. Скільки відрізків на прямій утворюють три різні точки?
А) 2; Б) 3; В) 4; Г) 6.
8.Точка X належить відрізку КМ. Серед променів МХ, МК, ХК, ХМ назвіть пари тих, що збігаються.
А) МХ, ХК; Б) ХМ, ХК; В) ХМ, МК; Г) МХ, МК.
9. Які з тверджень виражають основні властивості взаємного розміщення точок на прямій і на площині?
А) Якщо кінці відрізка належать одній (різним) півплощині то він не перетинає (перетинає) пряму.
Б) Яка б не була пряма, існують точки, що належать цій пря мій, і точки, що не належать їй.
В) Якщо точка С лежить між точками А і В, то вона розділж точки А і В.
Г) Пряма розбиває площину на дві півплощини.
10. Дано пряму і по дві точки в кожній з півплощин, на які вона розбиває площину. Скільки відрізків з кінцями в цих точкам перетинають пряму?
10. Дано пряму і по дві точки в кожній з півплощин, на які вона розбиває площину. Скільки відрізків з кінцями в цих точкам перетинають пряму?
А) 2; Б) 5; В) 4; Г) 3.
БАНК ЗАВДАНЬ
З ТЕМИ «НАЙПРОСТІШІ властивості ФІГУРИ »
14. Поясніть, що таке відрізок з кінцями у даних точках.
15. Сформулюйте основну властивість розміщення точок на прямій.
16. Сформулюйте основні властивості вимірювання відрізків.
17. Що називається відстанню між двома даними точками?
18. Які властивості має розбиття площини на дві півплощини?
19. Сформулюйте основну властивість розміщення точок відносно прямої на площині.
20. Скільки точок перетину можуть мати п’ятьвідрізків?
21. Що таке півпряма або промінь? Які півпрямі називаються доповняльними?
22. Як позначаються півпрямі?
23. Скільки рівних відрізків можна задати на промені?
24. Скільки променів можна задати на промені?
25. Які геометричні фігури не можна виміряти?
Тест "ОСНОВНІ ВЛАСТИВОСТІ ВИМІРЮВАННЯ ВІДРІЗКІВ І КУТІВ"
Тест "ОСНОВНІ ВЛАСТИВОСТІ ВИМІРЮВАННЯ ВІДРІЗКІВ І КУТІВ"
1. Яке з тверджень неправильне?
А) Кутом називається фігура, яка складається з двох різних півпрямих.
Б) Промінь проходить між сторонами даного кута, якщо він виходить з його вершини і перетинає якийсь відрізок з кінцям на сторонах цього кута.
В) Якщо сторони кута є доповняльними півпрямими однієї прямої, то кут називається розгорнутим.
Г) Якщо промінь с проходить між сторонами кута (аb), тo кут (аb) дорівнює сумі кутів (ас) і (bс).
2. Які з тверджень не виражають основні властивості вимірювання кутів?
А) Кожний кут має певну градусну міру, більшу від нуля.
Б) Градусна міра кута дорівнює сумі градусних мір кутів, н які він розбивається будь-яким променем, що проходить між йог сторонами.
В) Розгорнутий кут дорівнює 180°.
Г) Кути вимірюються градусами за допомогою транспортира.
3. Точки А, В, С лежать на одній прямій, причому АВ = 17 см, CB = 11 см, AС = 6 см. Яке з наведених тверджень правильне?
А) Точка А лежить між точками В і С.
Б) Точка В лежить на відрізку АС.
В) Точка С лежить справа від точки В.
Г) Точка С лежить між точками А і В.
4. Яку градусну міру має кут, якщо він становить п’ять шостих прямого кута?
А) 30°; Б) 75°; В) 15°; Г) 60°.
5. Промінь с проходить між сторонами кута (аb), який становить 90°. Чому дорівнюють кути (ас) і (bс), якщо кут (ас) в два рази більший за кут (bс)?
А) 20° і 70°; Б) 60° і 30°; В) 25° і 65°; Г) 35° і 55°.
6. На промені МN відкладено відрізок МР, більший за відрізок MN. Яка з трьох точок М, N, Р лежить між двома іншими?
А) М; В) N; Г) Р.
7. Яке твердження виражає основну властивість відкладання відрізків?
А) Кожний відрізок має певну довжину, більшу від нуля.
Б) Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою.
В) На будь-якій півпрямій від її початкової точки можна відкласти відрізок даної довжини і тільки один.
Г) Дві точки визначають єдиний відрізок.
8. На півпрямій АХ від точки А відклали відрізок АВ = 3см, а потім від точки В - відрізок ВС = 7 см. Яка довжина відрізка АС?
А) 3 см; Б) 4 см; В) 7 см; Г) 10 см.
9. Скільки на прямій МК існує точок, відмінних від К, для
яких МХ=МК?
яких МХ=МК?
А) Дві; Б) одна; В) жодної; Г) безліч.
10. Від прямої АВ у даній півплощини відклали кут ВАС = 30о і кут ВАD = 70°. Чому дорівнює кут СAD?
А) 100°; Б) 40°; В) 70°; Г) 30°.
БАНК ЗАВДАНЬ
З ТЕМИ «НАЙПРОСТІШІ властивості ФІГУРИ »
26. Яка фігура називається кутом?
27. Із скількох точок складається кут?
28. Із скількох променів складається пряма?
29. Із скількох променів складається кут?
30. Із скількох відрізків складається пряма?
31. Як позначається кут на площині? Накресліть кут АВС.
32. Який кут називається розгорнутим? Накресліть цей кут.
33. Який кут називається тупим? Накресліть цей кут.
34. Який кут називається гострим? Накресліть цей кут.
35. Який кут називається прямим? Накресліть цей кут.
36. Поясніть, що означає вираз: «Півпряма проходить між сторонами кута».
37. В яких одиницях вимірюють кути і за допомогою якого інструмента? Поясніть, як виконують вимірювання тупого кута.
38. Сформулюйте основні властивості вимірювання кутів.
39. Сформулюйте основні властивості відкладання відрізків і кутів.
40. Що таке трикутник?
41. Із скількох вершин складається трикутник?
42. Із скількох відрізків складається трикутник?
43. Із скількох точок складається трикутник?
44. Із скількох кутів складається трикутник?
45. Що таке кут трикутника при даній вершині?
46. Які відрізки називаються рівними?
47. Скільки рівних відрізків можна задати на довільному відрізку?
48. Які кути називаються рівними?
49. На скільки рівних кутів можна поділити променями довільний кут?
Тест "ІСНУВАННЯ ТРИКУТНИКА,
ЩО ДОРІВНЮЄ ДАНОМУ"
1. Яке з тверджень не є означенням трикутника?
А) Фігура, що складається з трьох точок А, В, С і відрізків АВ, ВС, СА, серед яких сусідні не лежать на одній прямій.
Б) Фігура, яка складається з трьох точок і трьох відрізків, що попарно сполучають ці точки.
В) Фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які попарно сполучають ці точки.
Г) ) Фігура, утворена замкненою ламаною лінією, що складається з трьох ланок.
2. Яке твердження неправильне?
А) Кутом трикутника МКР при вершині М називається кут, утворений півпрямими МК, МР.
Б) Два відрізки називаються рівними, якщо вони мають однакову довжину.
В) Два кути називаються рівними, якщо вони мають однакову кутову міру в градусах.
Г) Трикутники називаються рівними, якщо в них відповідні сторони рівні.
3. Відомо, що трикутник АВС рівний трикутнику МКР, кут А = 45°, кут В = 60°, кут С = 75°, ВС = 6 см. Чому дорівнює кут МРК?
А) 75°; Б) 60°; В) 45°; Г) 90°.
4. Яке з тверджень є основною властивістю існування трикутника, що дорівнює даному?
А) Для будь-якого трикутника існує трикутник, що дорівнює йому.
Б) Трикутники називаються рівними, якщо в них відповідні сторони і кути рівні.
В) Який би не був трикутник, існує трикутник, що дорівнює йому у заданому розміщенні відносно даної півпрямої.
Г) Два трикутники, які можна накласти один на одного так, щоб вони сумістилися, називають рівними.
5. Одна із сторін трикутника має довжину 18 см, периметр дорівнює 38 см. Які довжини двох інших сторін, якщо їх різниця дорівнює 6 см?
А) 26 см, 7 см; Б) 14 см, 13 см; В) 13 см, 7 см; Г) 18 см, 7 см.
6. Яке з тверджень є означенням паралельних прямих?
А) Дві прямі, які не перетинаються.
Б) Дві прямі на площині, якщо вони не перетинаються.
В) Дві прямі, які не мають спільної точки.
Г) Дві прямі, які збігаються.
7. Яке з тверджень є основною властивістю паралельних прямих?
А) Через точку, що не лежить на даній прямій, можна провести на площині не більш як одну пряму, паралельну даній;
Б) через точку проходить не більш як одна пряма, що не перетинається з даною прямою;
В) через точку, взяту поза прямою, проходить тільки одна пряма, паралельна даній;
Г) через точку, взяту поза прямою, можна провести пряму, паралельну даній.
8. Знайдіть за допомогою лінійки й косинця всі пари паралельних прямих на малюнку.
А) a\\n; Б) а\\n; d\\l; В) а\\l; m\\р; Г) а\\b.
9. Яке твердження неправильне?
А) Якщо пряма а перпендикулярна прямій b, а пряма с перпендикулярна прямій d, то пряма а паралельна прямій с.
Б) Якщо пряма а паралельна прямій b, то пряма b паралельна прямій а.
В) Якщо пряма а перпендикулярна прямій с і пряма b перпендикулярна прямій с, то пряма а паралельна прямій b.
Г) Якщо пряма а паралельна прямій b, а пряма b паралельна прямій с, то пряма а паралельна прямій с.
10. Яке твердження неправильне?
А) Основні властивості найпростіших фігур — аксіоми не доводяться і є вихідними при доведенні інших властивостей фігур.
Б) Під час доведення теорем дозволяється користуватися тільки аксіомами, а також вже доведеними властивостями — теоремами.
В) При доведенні теорем можна використовувати властивості фігур, які видно з малюнка.
Г) Формулювання теореми звичайно складається з двох частин: в одній говориться про те, що дано, у другій - про те, що має бути доведено.
БАНК ЗАВДАНЬ
З ТЕМИ «НАЙПРОСТІШІ властивості трикутника»
50. Які трикутники називаються рівними?
51. Чи вірно, що два трикутники рівні, якщо у них рівні тільки відповідні кути?
52. Чи вірно, що два трикутники рівні, якщо у них рівні відповідні сторони?
53. Чи може пряма перетинати усі три сторони трикутника?
54. Чи може пряма перетинати тільки одну сторону трикутника?
55. Як позначають на малюнку відповідні сторони і кути рівних трикутників?
56. Скільки пар рівних трикутників може утворитися у квадраті, якщо з’єднати відрізками протилежні вершини?
57. Скільки пар рівних трикутників може утворитися у прямокутнику, якщо з’єднати відрізками протилежні вершини?
58. Поясніть за власним малюнком існування трикутника, що дорівнює даному. Виписати рівні основні елементи рівних трикутників.
59. Чи існують нерівні між собою сторони у рівних трикутників?
60. Чи існують рівні між собою трикутники зі сторонами 1 см , 2 см , 3 см ? Чому це сталося?
61. Чи існують рівні між собою трикутники з кутами 51о, 59о, 71о? Чому це сталося?
62. Яка умова виконується на три сторони трикутника?
63. Який трикутник називається гострокутним? Накресліть цей трикутник.
64. Який трикутник називається прямокутним? Накресліть цей трикутник.
65. Який трикутник називається тупокутним? Накресліть цей трикутник.
66. Який трикутник називається різностороннім? Накресліть цей трикутник.
67. Який трикутник називається рівностороннім? Накресліть цей трикутник.
68. Який трикутник називається правильним? Накресліть цей трикутник.
69. Який трикутник називається рівнобедреним? Накресліть цей трикутник.
70. Який трикутник має суму кутів, що рівна двом прямим кутам? Накресліть цей трикутник.
71. Які прямі називаються паралельними?
72. Які відрізки називаються паралельними?
73. Який відрізок являється відстанню між паралельними прямими?
74. Чому дорівнює кут між паралельними прямими?
75. Які прямі називаються перпендикулярними?
76. Які відрізки називаються перпендикулярними?
77. Яким знаком позначають перпендикулярність прямих?
78. Яким знаком позначають паралельність прямих?
79. Скільки прямих і розгорнутих кутів утворюють дві перпендикулярні прямі?
80. Скільки трикутників можуть утворити чотири непаралельні між собою прямі? Розгляньте усі можливі випадки.
81. Скільки трикутників можуть утворити чотири точки на площині? Розгляньте усі можливі випадки.
82. Сформулюйте основну властивість паралельних прямих.
83. Наведіть приклад довільної аксіоми та приклад теореми.
Рівень Б. Середня складність завдань.
ПРЯМА, ТОЧКА, ВІДРІЗОК.
1. а) Проведіть пряму m. Позначте яку-небудь точку А, що лежить на прямій m, і точку В, що не лежить на прямій n.
2. б) Проведіть дві прямі а і b, що перетинаються. Позначте точку С перетину прямих; точку А на прямій a, що не лежить на прямій b; точку D, що не лежить на жодній з прямих а і b.
3. Позначте на аркуші паперу дві точки С і А. Проведіть через них пряму від руки. За допомогою лінійки перевірте правильність побудови.
4. Чи можуть дві різні прямі мати: а) дві точки; б)одну точки перетину? Поясніть відповідь.
5. Для перевірки правильності лінійки використовують такий спосіб. Через дві точки за допомогою лінійки проводять лінію. Потім лінійку перевертають і через ті самі точки знову проводять лінію. Якщо лінії не збіглися, то лінійка неправильна. На якій властивості прямих ґрунтується такий спосіб перевірки правильності лінійки?
6. Проведіть пряму а. Позначте на прямій m дві довільні точки А і В. Позначте тепер точку С так, щоб точка А лежала між точками В і С.
7. Проведіть пряму а. Позначте на ній дві довільні точки А і В. Позначте тепер яку-небудь точку С відрізка АВ.
8. Точка М лежить на прямій СD між точками С і D. Знайдіть довжину відрізка СD якщо:
1) СМ = 2,5 см, DM = 3,5 см;
2) СМ ж 3,1 дм, МD = 4,6 дм;
3) СМ = 12,3 м, МD> = = 5,8 м.
9. Позначте на прямій n дві точки F та E і поставте на око середину відрізка. Перевірте правильність побудови вимірювання за допомогою лінійки.
10. Три точки А, В,С лежать на одній прямій. Відомо, що АВ = 4,3 см, АС = 7,5 см, ВС = 3,2 см. Чи може точка А лежати між точками В і С? Чи може точка С лежати між точками А і В? Яка з трьох точок А, В, С лежить між двома іншими?
11. Точки А, В, С лежать на одній прямій. Чи належить точка В відрізку АС, якщо: АС = 5 см, ВС = 7 см? Поясніть відповідь.
12. Точки А, В, С лежать на одній прямій. Чи може точка В розділяти точки А і С, якщо: АС «* 7 см, ВС = 7,6 см? Відповідь поясніть.
13. Чи можуть точки А, В, С лежати на одній прямій, якщо АВ = 1,8 м, АС = 1,3 м, ВС = 3 м? Поясніть відповідь.
14. Чи можуть три точки А, В, С лежати на одній прямій, якщо довжина більшого відрізка АВ менша за суму довжин відрізків АС і ВС? Поясніть відповідь.
15. Точки А, В, С лежать на одній прямій. Знайдіть довжину відрізка ВС, якщо АВ = 2,7 м, АС = 3,2 м. Скільки розв'язків має задача?
16. На відрізку АВ довжиною 15 м взято точку С. Знайдіть довжини відрізків АС і ВС, якщо: 1) відрізок АС на 3 м довший за відрізок ВС; 2) відрізок АС у два рази довший за відрізок ВС; 3) точка С - середина відрізка АВ; 4) довжини відрізків АС і ВС відносяться, як 2 : 3.
17. Проведіть пряму m і позначте яку-небудь точку А, що не лежить на цій прямій. Позначте тепер дві точки В і С так, щоб відрізок АВ перетинав пряму m, а відрізок ВС не перетинав її.
18. Дано пряму і три точки А, В, С, що не лежать на цій прямій n. Відомо, що відрізок АВ перетинає пряму, а відрізок АС не перетинає її. Чи перетинає пряму відрізок ВС? Відповідь поясніть.
19. Дано пряму m і чотири точки А, В, С і D, що не лежать на цій прямій. Чи перетинає відрізок АD пряму, якщо:
1) відрізки АВ, ВС і СВ перетинають пряму;
2) відрізки АС і ВС перетинають пряму, а відрізок ВD не перетинає;
3) відрізки АВ і СD перетинають пряму, а відрізок ВС не перетинає;
4) відрізки АВ і СD не перетинають пряму, а відрізок ВС перетинає;
5) відрізки АВ, ВС, СD не перетинають пряму;
6) відрізки АС, ВС і DО перетинають пряму? Поясніть відповідь.
20. Дано п'ять точок і пряма, що не проходить через жодну з цих точок. Відомо, що три точки лежать в одній півплощині відносно цієї прямої, а дві точки — в іншій півплощині. Кожну пару точок сполучено відрізком. Скільки відрізків перетинає пряму? Відповідь поясніть.
21. Дано пряму а і точки А, X, Y, Z на цій прямій. Відомо, що точки X і Y лежать по один бік від точки А, точки X і Z, також лежать по один бік від точки А. Як розміщені точки Y і Z. відносно точки А: по один бік чи по різні боки? Поясніть відповідь.
ПРОМІНЬ, КУТ.
22. Позначте дві точки А і В. Проведіть півпряму АВ.
23. На відрізку АВ взято точку С. Серед півпрямих АВ, АС, СА, СВ назвіть пару півпрямих, які збігаються, і пару доповняльних півпрямих. Поясніть відповідь.
24. Проведіть з однієї точки три довільні промені. Визначте на око кути, утворені цими променями. Перевірте ваші відповіді, вимірюючи кути транспортиром. Виконайте вправу повторно.
25. Промінь а проходить між сторонами кута (сd). Знайдіть кут (сd), якщо:
1) кут (ас) = 35°, кут (аd) = 75°;
2) кут (ас) = 57° , кут(аd) = 62°;
3) кут (ас) = 94°, кут (аd) = 85°.
26. Чи може промінь с проходити між сторонами кута (ab), якщо:
1) кут (ас) = 30°, кут (сb)= 80°, кут (аb) = 50°;
2) кут (bс) = 100°, кут (сb) = 90°;
3) кут (ас) більший за кут (аb)?
27. Між сторонами кута (аb), що дорівнює 60°, проходить промінь с. Знайдіть кути (ас) і (bс), якщо:
1) кут (ас) на 30 більший за кут (bс);
2) кут (ас) в два рази більший за кут (bc);
3) промінь с ділить кут (аb) пополам;
4) градусні мір кутів (ас) і (bс) відносяться, як 2 : 3.
28. Проведіть пряму m. Позначте на цій прямій яку-небудь точку А. Потім візьміть на око точку В цієї прямої так, щоб АВ = 5 см. Перевірте точність побудови точки В лінійкою. Виконайте вправу повторно, якщо: 1) АВ = 3 см; 2) АВ = 7 см; 3) АВ= 10 см.
29. Побудуйте на око кути 30°, 45°, 60°, 90°. Перевірте точність побудови транспортиром. Виконайте вправу повторно.
30. Чи існує на півпрямій АВ така точка X, відмінна від В, що АХ = АВ? Поясніть відповідь.
31. На промені АВ відкладено відрізок АС, менший за відрізок АВ. Яка з трьох точок А, В, С лежить між двома іншими? Відповідь поясніть.
32. На промені АВ позначено точку С. Знайдіть довжину відрізка ВС, якщо: 1) АВ = 1,5 м, АС = 0,3 м; 2) АВ = 2 см, АС = 4,4 см.
РІВНІ ТРИКУТНИКИ.
33. Побудуйте на око трикутник з рівними сторонами (рівносторонній трикутник). Перевірте точність побудови вимірюванням сторін.
34. На стороні АВ трикутника АВС взято точку О. Чому дорівнює сторона АВ трикутника, якщо АО = 5 см, а ВО = 6 см?
35. На стороні АВ трикутника АВС взято точку О. Чому дорівнює кут С трикутника, якщо кут OCА = 30°, а кут BCO = 70°?
36. Накресліть довільний трикутник. Побудуйте від руки, на око, трикутник, що дорівнює йому. Перевірте правильність побудови, вимірюючи відповідні кути і сторони. Виконайте вправу повторно.
37. Трикутники АВС і РDF рівні. Відомо, що АВ = 5 см, ВС = 6 см, АС = 7 см. Знайдіть сторони трикутника РDF. Поясніть відповідь.
38. Трикутники АВС і EDF рівні. Кути другого трикутника відомі: кут Е = 40°, кут D = 60°, кут F = 80°. Знайдіть кути трикутника АВС.
39. Трикутники АВС і РDF рівні. Відомо, що сторона АВ дорівнює 10 м, а кут С = 90°. Чому дорівнює сторона РD і кут F? Поясніть відповідь.
40. Трикутники АВС, РDF і ХYZ рівні. Відомо, що АВ = 5 см,
PD = 6 см, ZХ = 7 см. Знайдіть решту сторін кожного трикутника.
41. Дано трикутник АВС. Чи існує інший трикутник, що дорівнює трикутнику АВС?
42. Чи може пряма, що перетинає одну з двох паралельних прямих, не перетинати другу? Поясніть відповідь.
43. Дано дві прямі, що перетинаються. Чи можна провести третю пряму, паралельну кожній з двох даних?
44. Чи може пряма, що не проходить через жодну з вершин трикутника, перетинати кожну його сторону? Чому?
45. Дано чотири точки: А, В, С і В. Відомо, що точки А, В, С лежать на одній прямій і точки В, С, N також лежать на одній прямій. Доведіть, що всі чотири точки лежать на одній прямій.
46. Дано чотири прямі а, b, с і d. Відомо, що прямі а, b, с перетинаються в одній точці й прямі b, с, d також перетинаються в одній точці. Доведіть, що всі чотири прямі проходять через одну точку.
47. Точки А, В, С, D не лежать на одній прямій. Відомо, що
пряма АВ перетинав відрізок СD, а пряма СD перетинає
відрізок АВ. Доведіть, що відрізки АВ і СD перетинаються.
пряма АВ перетинав відрізок СD, а пряма СD перетинає
відрізок АВ. Доведіть, що відрізки АВ і СD перетинаються.
КУТИ
СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ
1. Яке твердження неправильне?
А) Якщо сторони кута є доповняльними півпрямими однієї прямої, то кут називається розгорнутим.
Б) Два кути називаються суміжними, якщо в них одна сторона спільна.
В) Прямим кутом називають кут, що дорівнює 90°.
Г) Кут, менший за 90°, називається гострим кутом.
2. Один із суміжних кутів дорівнює 30°. Чому дорівнює другий кут?
А) 60°; Б) 150°; В) 90°; Г) 30°.
3. Скільки кутів, суміжних з даним, можна побудувати?
А) 1; Б) 2; В) 3; Г) 4.
4. Яке твердження неправильне?
А) Якщо даний кут прямий, то суміжний з ним кут гострий.
Б) Якщо один із суміжних кутів прямий, то ці кути рівні.
В) Якщо даний кут тупий, то суміжний з ним кут гострий.
Г) Кут, більший за 90° і менший від 180°, називається тупим кутом.
5. Один із суміжних кутів у 7 разів більший другого. Знайдіть величину більшого кута.
А) 22,5°; Б) 157,5°; В) 156,5°; Г) 167,5°.
ПЕРПЕНДИКУЛЯРНІ ПРЯМІ.
ДОВЕДЕННЯ ВІД СУПРОТИВНОГО.
1. Побудуй два різних відрізки, що мають спільну точку. Які з пар кутів на твоєму малюнку є вертикальними?
А) кут ВОС і кут КОЕ; Б) кут РОВ і кут СОЕ; В) кут СOD і кут СОА; Г) кут СОЕ і кут АОВ.
2. Один з вертикальних кутів, утворених при перетині двох прямих, дорівнює 30°. Чому дорівнює друга пара вертикальних кутів?
А) 150°; Б) 30°; В) 60°; Г) 160°.
3. Яке твердження неправильне?
А) Вертикальні кути рівні.
Б) Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
В) Перпендикуляром до прямої називається відрізок прямої, перпендикулярної до даної.
Г) Через кожну точку прямої можна провести перпендикулярну до неї пряму і до того ж тільки одну.
4. Сума однієї пари вертикальних кутів, утворених при перетині двох прямих, дорівнює 180°. Чому дорівнює кожний з цих кутів?
А) 90° і 90°; Б) 80° і 100°; В) 140° і 40°; Г) 70° і 110°.
5. Один із двох кутів, які утворюються при перетині двох прямих, в три рази більший від другого. Знайдіть кожний з цих кутів.
А) 45° і 135°; Б) 60° і 180°; В) 30° і 90°; Г) 40° і 160°.
КУТИ, ВІДКЛАДЕНІ В ОДНІЙ ПІВПЛОЩИНІ.
1. Дано кут (аb). Промінь с, який виходить з його вершини, перетинає відрізок з кінцями на сторонах кута. Як розміщений промінь с щодо сторін кута?
А) Не проходить між його сторонами.
Б) Доповняльний до променя а.
В) Перетинає промінь b.
Г) Проходить між його сторонами.
2. Від півпрямої у даній півплощині треба відкласти кут із за даною градусною мірою. Скільки таких кутів можна відкласти?
А) Два; Б) безліч; В) один; Г) жодного.
3. Яке твердження неправильне?
А) Два кути називаються суміжними, якщо в них одна сторона спільна, а інші сторони цих кутів є доповняльними півпрямими.
Б) Два кути називаються вертикальними, якщо сторони одного кута є доповняльними півпрямими сторін другого.
В) Якщо від даної півпрямої відкласти в одній півплощині два різні кути, то сторона більшого кута, відмінна від даної півпрямої, проходить між сторонами меншого.
Г) Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
4. Кут (аb) = 40°, кут (ас) = 90°, а промені b і с лежать в одній півплощині. Чому дорівнює кут (bс)?
А) 130°; Б) 40°; В) 90°; Г) 50°.
5. Між сторонами кута (аb), що дорівнює 80°, проходить промінь. Знайдіть кут (ас), якщо кут (сb) у три рази менший за кут (ас).
А) 60°; Б) 20°; В) 40°; Г) 80°.
ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ
ПЕРША ОЗНАКА РІВНОСТІ ТРИКУТНИКІВ
1. Яке з тверджень не є аксіомою?
А) Який би не був трикутник, існує трикутник, що дорівнює йому у заданому розміщенні відносно даної півпрямої.
Б) Якщо пряма, яка не проходить через жодну з вершин трикутника, перетинає одну з його сторін, то вона перетинає тільки одну з двох інших сторін.
В) На будь-якій півпрямій від її початкової точки можна відкласти відрізок даної довжини і тільки один.
Г) Від будь-якої півпрямої у даній півплощині можна відкласти кут з даною градусною мірою, меншою 180°, і тільки один.
2. Відрізки АВ = 6 см і СD = 10 см перетинаються в точці О, яка є серединою кожного з них. Чому дорівнює відрізок AD?
А) 6 см; Б) СВ; В) 10 см; Г) 5 см.
3. Яке твердження неправильне?
А) Два відрізки називаються рівними, якщо вони мають однакову довжину.
Б) Два кути називаються рівними, якщо вони мають однакову кутову міру в градусах.
В)Трикутником називається фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які попарно сполучають ці точки,
Г) Трикутники називаються рівними, якщо в них рівні відповідні кути.
4. У трикутниках АВС і А1В1С1, АВ=А1В1 = 7 см, АС = А1С1 = 7 см, кут А = кут А1 = 60°. Яка з рівностей правильна?
А) трикутник АСВ = трикутник А1В1С1 ;
Б) трикутник АСВ = трикутник А1В1С1;
В) трикутник АВС = трикутник В1А1С1;
Г) трикутник АВС = трикутник А1В1С1
5. У трикутниках АВС і АКС кут ВСА = кут КСА; ВС = КС =1,5 см. Яка рівність правильна?
А) трикутникАВС = трикутник АСК;
Б) трикутник АВС = трикутник САК;
В) трикутник АВС = трикутник АКС;
Г) трикутник АВК= трикутник ВСК.
ДРУГА ОЗНАКА РІВНОСТІ ТРИКУТНИКІВ.
1. Яке з наведених тверджень не є аксіомою?
А) Який би не був трикутник, існує трикутник, що дорівнює йому в заданому розміщенні відносно даної півпрямої.
Б) На будь-якій півпрямій від її початкової точки можна відкласти відрізок даної довжини і тільки один.
В) Від будь-якої півпрямої у даній півплощині можна відкласти кут з даною градусною мірою, меншою 180°, і тільки один.
Г) Якщо сторона і прилеглі до неї кути одного трикутника дорівнюють відповідно стороні й прилеглим до неї кутам другого трикутника, то такі трикутники рівні.
2. У трикутниках АВС і МРК АС=МК, кут А = кут М, кут С = кут С1. Згідно з яким твердженням ці трикутники рівні?
А) Другою ознакою рівності трикутників.
Б) Першою ознакою рівності трикутників.
В) Аксіомою існування трикутника, що дорівнює даному.
Г) Аксіомою відкладання кутів.
3. Дано два трикутника АВС і ХYZ, у яких АВ = ХY, кут А = = кут Х, кут В = кут Y. Яка з рівностей неправильна?
А) трикутник АВС = трикутник ХYZ; Б) ВС = YZ; В) кут А = кут Z; Г) кут С = кут Z.
4. Відрізки АВ і А1В1 перетинаються в точці С, ВС = АС, кут А = кут В. Яка з рівностей неправильна?
1) трикутник АА1С = трикутник ВВ1С;
2) трикутник САА1 = трикутник В1СВ;
3) В1С = СА1;
4) кут А1 = кут В1.
5. АВ = ВС, кут А = кут С. Яка з рівностей неправильна?
А) трикутник АВЕ = трикутник СВD; Б) кут В = кут D; В) АE=СD;
Г) кут D = кут E.
РІВНОБЕДРЕНИЙ ТРИКУТНИК
1. Який з трикутників, що ви виконали у своєму зошиті, є рівнобедреним?
А) трикутник АВD; Б) трикутник АDE; В) трикутник ВЕD; Г) трикутник ВEС.
2. Трикутник САВ дорівнює трикутнику СВА. Яка з рівностей щодо кутів цих трикутників правильна?
А) кут А = кут С; Б) кут В = кут С; В) кут А = кут В; Г) кут А = кут В = кут С.
3. У трикутнику АВС (АВ = ВС) сторони АС і ВС продовжено у різні сторони. Яка з рівностей правильна?
А) кут А= кут В Б) кут В = кут С В) кут А= кут АСЕ; 4) кут DСЕ = кут А.
4. Периметр рівнобедреного трикутника дорівнює 10 см, його основа 4 см. Чому дорівнює бічна сторона?
А) 3 см; Б) 6 см; В) 4 см; Г) 5 см.
5. Периметр рівнобедреного трикутника дорівнює 60 см, а бічна сторона 25 см. Чому дорівнює його основа?
А) 5 см; Б) 10 см; В) 35 см; Г) 17,5 см.
МЕДІАНА, БІСЕКТРИСА І ВИСОТА ТРИКУТНИКА.
1. Яке твердження неправильне?
А) Висотою трикутника, опущеної з даної вершини, називається перпендикуляр, проведений з цієї вершини до прямої, що містить протилежну сторону трикутника.
Б) Медіаною трикутника, проведеного з даної вершини, називається відрізок, що сполучає цю вершину із серединою протилежної сторони трикутника.
В) Перпендикуляром до даної прямої називається відрізок прямої, перпендикулярної до даної.
Г) Бісектрисою трикутника, проведеною з даної його вершини, називається відрізок бісектриси кута трикутника, що сполучає цю вершину з точкою на протилежній стороні.
2. Дано: трикутник АВС, АВ = 8 см, ВС = 10 см, АС = 9 см, СМ – медіана. Чому дорівнює відрізок МВ?
А) 4 см; Б) 5 см; В) 4,5 см; Г) 8 см.
3. Чому дорівнює бісектриса рівнобедреного трикутника АВС, проведена до основи АС, якщо медіана ВМ = 4 см, а висота СК = 6 см?
А) 4 см; Б) 6 см; В) 2 см; Г) 3 см.
4. У рівнобедреному трикутнику з вершин при його основі
проведено медіани. Яке твердження щодо них правильне?
проведено медіани. Яке твердження щодо них правильне?
А) Медіани різні; Б) дорівнюють висоті; В) рівні; Г) збігаються з бісектрисами.
5. У трикутнику СDЕ кут С = кут D. Медіана якої із сторін збігається з бісектрисою і висотою?
А) ЕD; Б) СЕ; В) DС; Г) СD.
ТРЕТЯ ОЗНАКА РІВНОСТІ ТРИКУТНИКІВ.
1. Яка теорема використовується при доведенні третьої ознаки рівності трикутників?
А) У рівнобедреному трикутнику кути при основі рівні.
Б) Якщо в трикутника два кути рівні, то він рівнобедрений.
В) У рівнобедреному трикутнику медіана, проведена до основи, є його бісектрисою і висотою.
Г) Вертикальні кути рівні.
2. Трикутники АВС і КМР рівні за третьою ознакою рівності трикутників. Яка з рівностей неправильна?
А) АС = КР, АВ = КМ, кут А= кут К;
Б) ВС = КР, АС = КМ, кут С = кут М;
В) АС = КР, кут А = кут К, кут С = кут Р;
Г) АВ = КМ; ВС = МР; АС = КР.
3. Дано: трикутник АВС = трикутник А1В1С1. Периметр трикутника АВС дорівнює 12 см, АВ = 3 см, ВС = 4 см. Чому дорівнює сторона А1С1?
А) 3см; Б) 5 см; В) 4 см; Г) 7 см.
4. Якими будуть трикутники АВС
і КМР, якщо АВ = КМ, АС = КР, кут С=.
= кут Р?
і КМР, якщо АВ = КМ, АС = КР, кут С=.
= кут Р?
А) рівні; Б) нерівні; В) рівносторонні; Г) рівнобедрені.
5. Дано: трикутник АВD і трикутник DВС. Відомо, що АВ = АD і DС = ВС. Який із записів неправильний?
А) трикутник АВС = трикутник АDС;
Б) кут В = кут D;
В) ВD і АС перпендикулярні ;
Г) трикутник ВАD = трикутник ВСD.
Підписатися на:
Коментарі (Atom)










